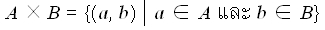บทที่ 4 ความสัมพันธ์และฟังก์ชัน

4.1ความสัมพันธ์และฟังก์ชัน

คู่อันดับ (Order Pair) เป็นการจับคู่สิ่งของโดยถือลำดับเป็นสำคัญ เช่น คู่อันดับ a, b จะเขียนแทนด้วย (a, b) เรียก a ว่าเป็นสมาชิกตัวหน้า และเรียก b ว่าเป็นสมาชิกตัวหลัง

(การเท่ากับของคู่อันดับ) (a, b) = (c, d) ก็ต่อเมื่อ a = c และ b = d

ผลคูณคาร์ทีเชียน (Cartesian Product) ผลคูณคาร์ทีเซียนของเซต A และเซต B คือ เซตของคู่อันดับ (a, b) ทั้งหมด โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B

สัญลักษณ์      ผลคูณคาร์ทีเซียนของเซต A และเซต B เขียนแทนด้วย A x B
หรือ เขียนในรูปเซตแบบบอกเงื่อนไขจะได้ว่า

 อ่านเพิ่มเติม

3.3 การนำสมบัติของจำนวนจริงไปใช้ในการแก้สมการกำลังสอง

3.3 การนำสมบัติของจำนวนจริงไปใช้ในการแก้สมการกำลังสอง

ตัวแปร    :  อักษรภาษาอังกฤษตัวเล็ก เช่น x , y ที่ใช้เป็นสัญลักษณ์แทนจำนวน

ค่าคงตัว  :  ตัวเลขที่แททนจำนวน เช่น 1, 2

นิพจน์    :  ข้อความในรูปสัญลักษณื เช่น 2, 3x  ,x-8 ,

เอกนาม  :  นิพจน์ที่เขียนอยู่ในรูปการคูณของค่าคงตัวแปรตั้งแต่หนึ่งตัวขึ้นไปที่มีเลขชี้                 กำลังของตัวแปรเป็นจำนวนเต็มบวกหรือศูนย์ เช่น -3, 5xy , 2y

พหุนาม :  นิพจน์ที่สามารถเขียนในรูปของเอกนาม หรือการบวกเอกนามตั้งแต่สองเอก   นามขึ้นไป เช่น 3x , 5x +15xy+10x+5

ดีกรีของเอกนาม : ดีกรีสูงสุดของเอกนามในพหุนามนั้น เช่น x+2xy+1 เป็นพหุนามดีกรี 3 อ่านเพิ่มเติม

3.2 สมบัติของจำนวนจริงเกี่ยวกับการบวกและการคูณ

3.2 สมบัติของจำนวนจริงเกี่ยวกับการบวกและการคูณ

1) สมบัตของการเท่ากันในระบบจำนวนจริง

         เมื่อ a, b , c เป็นจำนวนจริงใดๆ

(1)      สมบัติการสะท้อน a = a

(2)      สมบัติการสมมตรา ถ้า a = a แล้ว b = c

(3)      สมบัติการถ่ายทอด ถ้า a = a และb = c แล้ว a = c

(4)      สมบัติการบวกด้วยจำนวนที่เท่ากัน

ถ้า a = b แล้ว a+c = b+ c

         (5) สมบัติการคูณด้วยจำนวนที่เท่ากัน

              ถ้า  a =  b แล้ว ac = bc

 2) สมบัติการบวกและการคูณจำนวนจริง

            ถ้า a, b, c เป็นจำนวนจริงใดๆ อ่านเพิ่มเติม

บทที่ 3 จำนวนจริง

3.1จำนวนจริง

เซตของจำนวนจริงประกอบด้วยสับเซตที่สำคัญ  ได้แก่

- เซตของจำนวนนับ/ เซตของจำนวนเต็มบวก เขียนแทนด้วย  I

                   I = {1,2,3…}

- เซตของจำนวนเต็มลบ  เขียนแทนด้วย  I

- เซตของจำนวนเต็ม เขียนแทนด้วย I

                   I = { …,-3,-2,-1,0,1,2,3…}

- เซตของจำนวนตรรกยะ : เซตของจำนวนจริงที่สามารถเขียนได้ในรูปเศษส่วน      โดยที่ a,b เป็นจำนวนเต็ม  และ b = 0 อ่านเพิ่มเติม

บทที่ 2 การให้เหตุผล

การให้เหตุผลทางคณิตศาสตร์ที่สำคัญมีอยู่ 2 วิธี คือ

         3.1การให้เหตุผลแบบอุปนัย (Inductive Reasoning) เป็นการสรุปผลในการค้นหาความจริงจากการสังเกต  หรือการทดลองหลายครั้งจากกรณีย่อยๆ แล้วนำมาสรุปเป็นความรู้แบบทั่วไป ซึ่งข้อสรุปที่ไม่จำเป็นต้องถูกต้องทุกครั้ง

         3.2การให้เหตุผลแบบนิรนัย (Deductive Reasoning ) เป็นการนำสิ่งที่ยอมรับว่าเป็นจริงมาประกอบเพื่อนำไปสู่ข้อสรุปจากสิ่งที่ยอมรับแล้ว อ่านเพิ่มเติม 

1.4ยูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต

1.4ยูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต

- ยูเนียน (Union) : ยูเนียนของเซต A และเซต B จะได้เซตใหม่ ซึ่งมีสมาชิกของเซต A หรือเซต B  หรือทั้งสองเซต

   “ ยูเนียนของเซตA และเซต B เขียนแทนด้วย A   B ”

A   B = {x| x   A หรือ x เ ป็นสมาชิกของทั้งสองเซต}

เช่น A = {1,3,5} และ B = {3,6,9}

จะได้  A    B ={1,3,5,6,9}

- อินเตอร์เซกชัน (Intersection): อินเตอร์เซกชันของเซต A และเซต B จะได้เซตใหม่ ซึ่งสมาชิกเป็นสมาชิกของเซตทั้งเซต A และเซต B

   “ อินเตอร์เซกชันของเซตA และเซต B เขียนแทนด้วย A    B อ่านเพิ่มเติม

1.3 สับเซตและเพาเวอร์เซต

1.3 สับเซตและเพาเวอร์เซต

เซต A เป็นสับเซตของเซต B ก็ต่อเมื่อ  สมาชิกทุกตัวของ A เป็นสมาชิกของ B เขียนแทนด้วย AB เซต A ไม่เป็นสับเซตของเซต B ก็ต่อเมื่อ มีสมาชิกอย่างน้อยหนึ่งตัวของเซต A ที่ไม่ป็นสมาชิกของเซต B เขียนแทนด้วย AB เช่น

A = {3,5} และ B = {1,3,5,7,9}

จะได้ว่า  A     B แต่ B  A

สมบัติของสับเซต

1.            A  A และ   A

2.            ถ้าAB และ BC แล้วAC

3.            ACและ BC ก็ต่อเมื่อ A = B

อ่านเพิมเติม